時間複雜度和空間複雜度是衡量演算法效率的重要指標,較低的時間複雜度可以使演算法更快地運行而較低的空間複雜度可以更有效地利用計算資源。當資料量一多時,有效的計算時間複雜度以及空間複雜度可以提高應用程式的性能。因此,時間複雜度和空間複雜度是優化應用程式效能的關鍵。
“n”和”O” 符號
演算法中的”n“表示是需要處理的資料量(nums.length)。假設以下list中有5個元素,總共有5筆資料需要處理。那n就是等於5。
listA = [1, 2, 3, 4, 5]在進行時間複雜度分析時, “O” 符號來表示演算法的時間複雜度的上限(最壞時間複雜度,考慮演算法執行時所需要的最多執行步驟數),而 “Ω” 符號來表示演算法的時間複雜度的下限(最佳時間複雜度,考慮演算法執行時所需要的最少執行步驟數)。
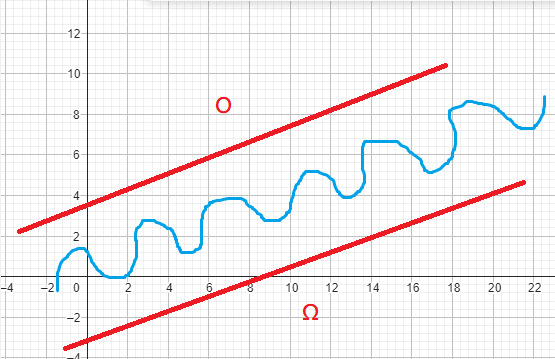
假設一個演算法的時間複雜度為 O(n),那就是代表當資料量是 n 時,演算法的時間複雜度的上限為 n。
每寫一行程式碼都是一個動作,假設在資料長度為5的for 迴圈前有兩個操作,Example: hashtable = {}, for 迴圈需要操作5次,因此for 迴圈總共需要 5n次操作,再加上前兩次的操作,總共操作次數為5n+2。那時間複雜度為 O(5n+2),時間複雜度為 5n+2 的算法可以將時間複雜度簡化為 O(n)。
O(n)及O(n2)
O(n)是直接查找,如果要查找的元素剛好就在list的第0位,那很幸運就是1,如果所要查找的元素不幸的就在list的第最後一位(n),那時間複雜度最壞的情況就是O(n)了。
O(n2)則是先排序在查找,假設把list中的數字先從小排到大後再去查找資料,由於每一筆在排序時需要和下一個數字去比大小,確保最小的值在list的第一位,總共需要的步驟數為(n+(n-1)+(n-2)+……一直加上最後一個步驟((n-(n-1))為1,所以是n * (n+1) / 2個步驟 ,最後再把比完的數字較小的丟到左邊,有n個就做n次,最後的total是是n * (n+3) / 2 (由 n * (n+1) / 2 + n而來 )簡化為 O(n2)。
以Leetcode的第一題 Two Sum的問題來說,Constraints給的資料量是介於 2 <= n <= 104。

時間複雜度 O(n)的算法就會比O(n2)來的好 ,因為若是最大資料量長度為104時 ,時間複雜度O(n2)為O(108)需要花得時間會比時間複雜度O(n)的O(104)花得時間還要長。
O(logn)及O(nlogn)
O(log n) 是指當n 增加時,算法的時間複雜度隨著 n 以對數(logarithm)的速度增加n = 2x。假設,當 n = 8,那只需3個步驟就可以完成,若n 增加到1024 時,程式會在 10個步驟完成。這通常出現在能夠將尋找的target範圍逐步縮小的算法中,如二分搜尋(binary search)。小時候玩的終極密碼, 依照提示可以將每次查找的區間縮小一半就是一種二分搜尋法。
O(nlogn)是指當n 增加時,算法的時間複雜度隨著n 乘以對數(logarithm)的速度增加。假設,當 n = 8,那只需24個步驟就可以完成(8*3),若n 增加到1024 時,程式會在 100個步驟完成(10*10)。如大部分的sort都皆為O(nlogn),如 quick sort。
O(n!)及O(C(k, n))及O(2n)
O(n!): n! 為階乘(n(n-1)(n-2)…..1),當 n=10 時,n! 的值為3628800。這種時間複雜度通常出現在需要獲得所有組合的時候,適合用在n較小的情況下,否則時間複雜度將變得非常高。
O(C(k, n)): C(k, n) 表示在 n 個元素中取出 k 個元素的組合數。當 n 和 k 相等時,C(k, n) 的值等於 1,因為只有一種可能的組合,時間複雜度是 O(1),這種時間複雜度通常出現在需要獲得所有可能的組合的時候 。O(C(k, n))計算公式為 n! / (k! * (n-k)!),當要在5 個元素中取出 4 個元素的組合數時間複雜度為5,當要在5個元素中取出 2個元素的組合數時間複雜度為O(5)
O(2n): 當 n 增加時,時間複雜度將以指數級別增加。當 n=10 時,2n的值是 1024,當 n=20 時, 2n的值則為1048576。