Backtracking(回溯)是一種用於尋找所有解決特定計算問題的答案,特別是在涉及限制滿足問題或解決策問題的情況。
Backtracking 是Top-down的寫法,從可能解的根開始探索解空間的樹。當在到達某個Node並發現該Node不能導致可能的解時則會回退(Backtracking到前一個Node),並探索新的路徑。這種算法的特點是嘗試建立一種解決方案,如果最新的解決方案不能成功,則取消(或Backtracking )最後的步驟並嘗試另一種可能的解決方案。在這個算法中,我們必須去思考每個點必須做什麼。
Backtracking 就像走迷宮,嘗試一條路徑,如果這條路徑走不通就回到前一個路口,然後嘗試另一條路徑。像這樣無法預知下一層狀態時,就只能用暴力解方式去解出來了。
489. Robot Room Cleaner
這提示是 Backtracking 的經典例題。
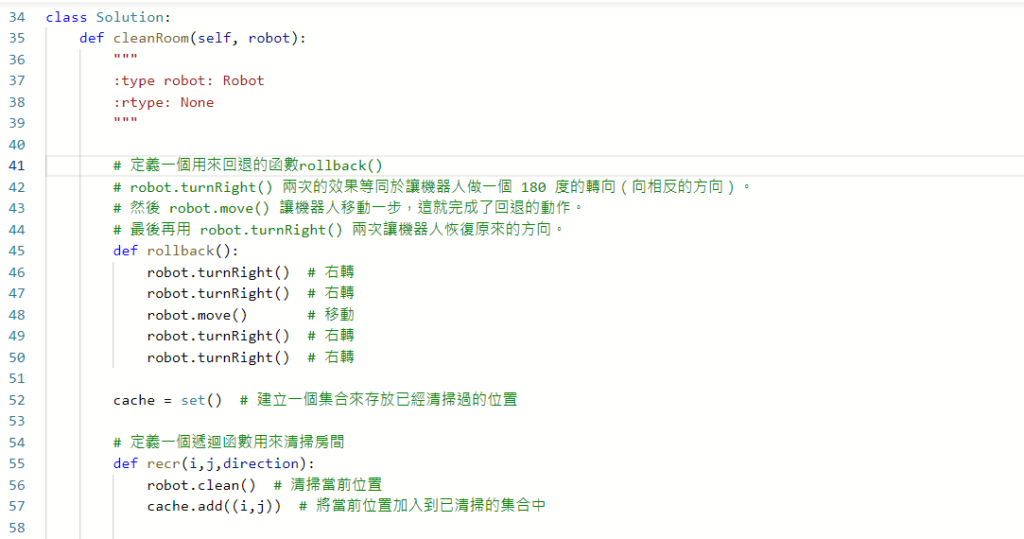

在函數調用後,必須將變量rollback到這一層的預期值。
37. Sudoku Solver

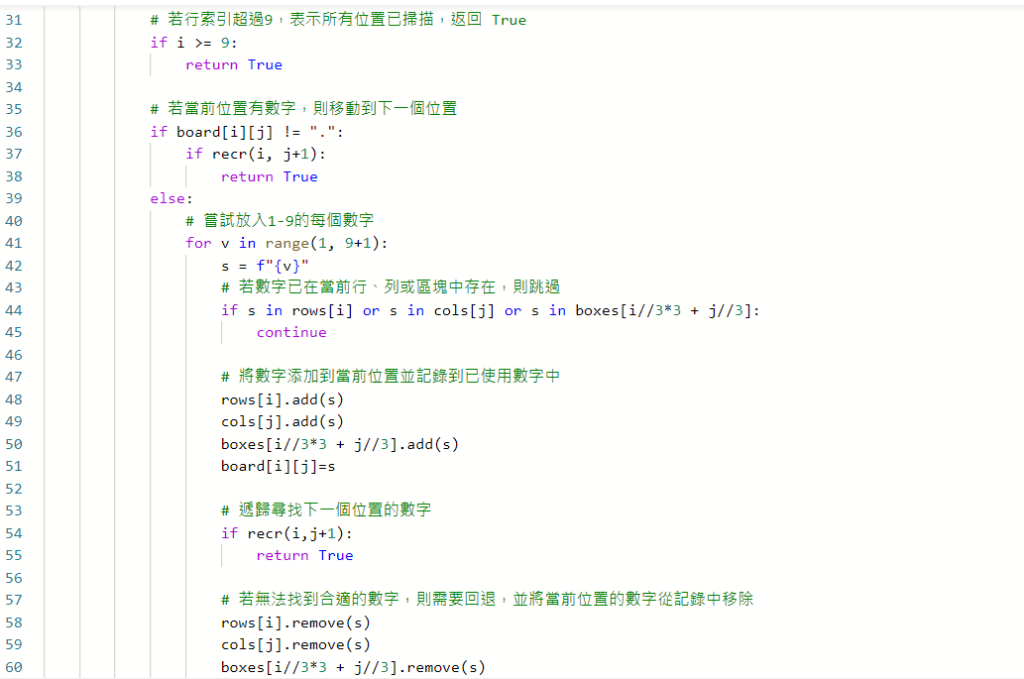

boxes[i//3*3 + j//3].add(board[i][j])
i//3*3 + j//3 是用來計算 (i, j) 這個位置對應到哪一個小網格。
i//3*3 是將行數 i 分為上中下三部分
j//3 是將列數 j 分為左中右三部分,兩者相加就能得到 (i, j) 對應的小網格索引。
位置 (5, 7),則對應的小網格索引就是 5//3*3 + 7//3 = 4,表示這個位置對應到的小網格是第4個。

79. Word Search

46. Permutations

46. Permutations backtracking + bitmask寫法
