Binary Search是一種在有序數列中查找特定值的演算法。
- 在有序數列中找到中間的元素。
- 如果這個元素恰好是我們正在尋找的值,那麼搜索就結束了。
- 如果目標值比中間元素大,那麼可以在數列的右半部(即比中間元素大的部分)繼續搜索。
- 如果目標值比中間元素小,則在數列的左半部(即比中間元素小的部分)繼續搜索。
在新的範圍內重複上述步驟,直到找到要尋找的元素,或者搜索範圍已經不存在。
二分搜尋法的效率很高,時間複雜度為 O(log n), n 是數列的元素數量。這是因為每一步都將搜索範圍減半,因此即使在大型數據集中,二分搜尋法也可以很快地找到目標值。
假設排序數組的長度是109。
沒有二分查找:O(109)
使用二分查找: O(log(109)) = O(29.897352854) ~= O(30)
但二分搜尋法的前提是數列必須已經排序。如果數列是無序的,我們需要先將它排序,否則無法使用二分搜尋法。
bisect_left & bisect_right
bisect_left 會找出在保持排序的情況下,新的數字可以被插入的最左邊的位置。如果這個新的數字已經在列表中存在,bisect_left 會返回這個數字現有位置的最左邊。
bisect_right 函數會找出在保持排序的情況下,新的數字可以被插入的最右邊的位置。如果這個新的數字已經在列表中存在,bisect_right 會返回這個數字現有位置的右邊一個位置。
bisect_left 傾向於在左邊插入新的數字,而 bisect_right 傾向於在右邊插入新的數字。
import bisect
nums = [1, 3, 4, 4, 6, 8]
# 使用 bisect_left 尋找 4 的位置
print(bisect.bisect_left(nums, 4)) # 輸出:2,因為在索引 2 的位置就是我們的第一個 4。
# 使用 bisect_right 尋找 4 的位置
print(bisect.bisect_right(nums, 4)) # 輸出:4,這是數字 4 可以插入的最右邊的位置,而不會破壞列表的排序。
# 使用 bisect_left 尋找 7 的位置
print(bisect.bisect_left(nums, 7)) # 輸出:5,這是數字 7 可以插入的最左邊的位置,而不會破壞列表的排序。
# 使用 bisect_right 尋找 7 的位置
print(bisect.bisect_right(nums, 7)) # 輸出:5,這是數字 7 可以插入的最右邊的位置,而不會破壞列表的排序。
binary_search寫法
def binary_search(arr, target):
# 定義i跟j,要涵蓋所有可能
i = 0
j = len(arr) - 1
# while 迴圈 只要 i 不大於 j,就繼續搜索
while i <= j:
mid = i + (j - i) // 2 # 取中點
# 定義condition function or if,將mid並帶入,利用結果來移動i跟j
if arr[mid] == target: # 如果找到目標,就返回中點的位置
return mid
elif arr[mid] < target: # 如果中點的值小於目標,就在右半部分繼續尋找
i = mid + 1
else: # 如果中點的值大於目標,就在左半部分繼續尋找
j = mid - 1
return -1 # 如果沒有找到目標,就返回 -1
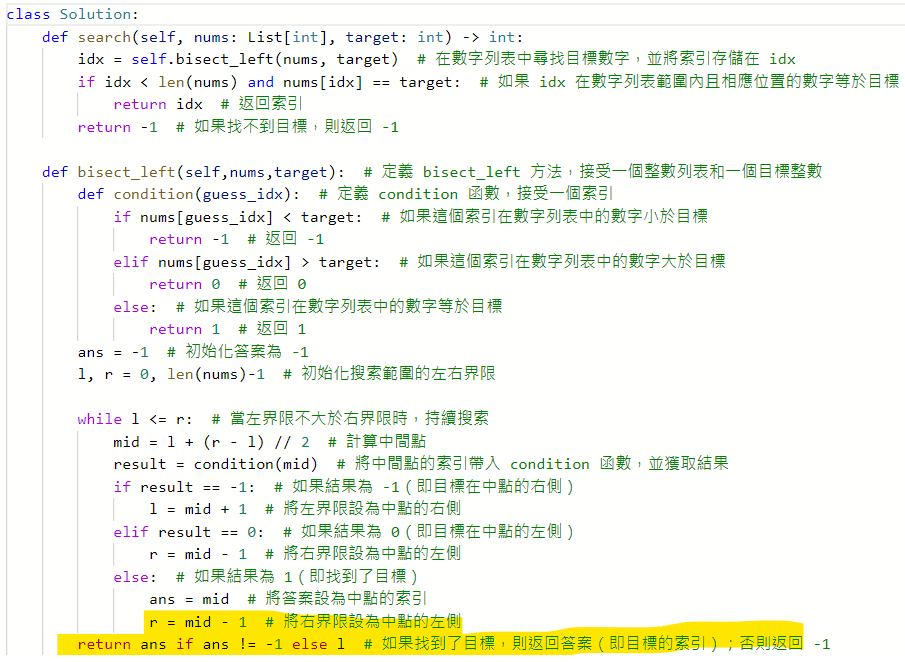
704. Binary Search

python套件
- import bisect
- bisect_left(array, target)
- bisect_right(array, target)


153. Find Minimum in Rotated Sorted Array
不用bisect_left or bisect_right的解法

bisect_right -1
bisect_right(target) – 1 可以用來找接近(小於)的特定值
167. Two Sum II – Input Array Is Sorted


410. Split Array Largest Sum

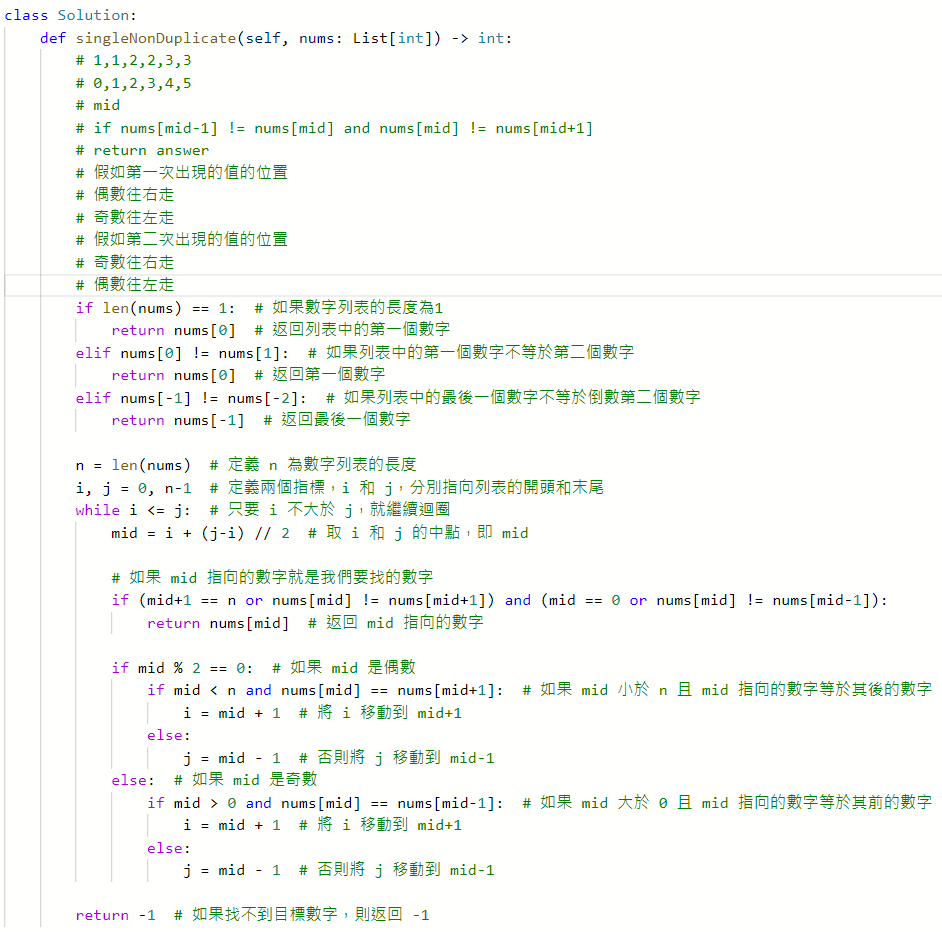
540. Single Element in a Sorted Array
1146. Snapshot Array

35. Search Insert Position

367. Valid Perfect Square

162. Find Peak Element

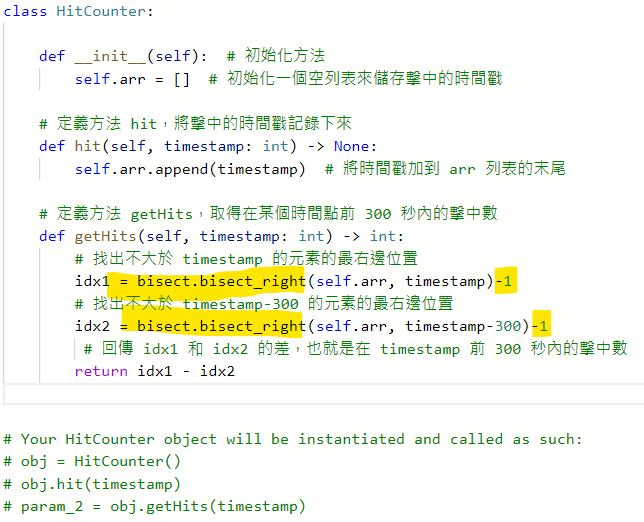
981. Time Based Key-Value Store
