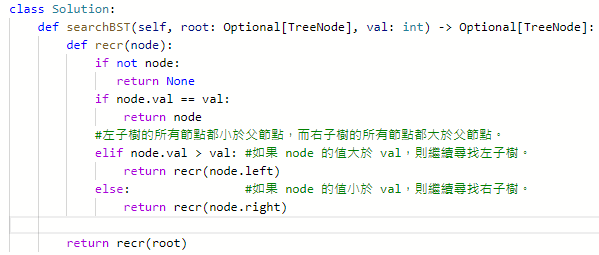
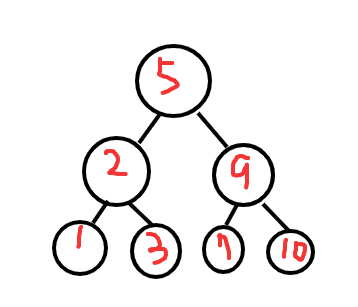
Common trees有以下幾種
- Full binary tree:每個節點都有零個或兩個子節點。
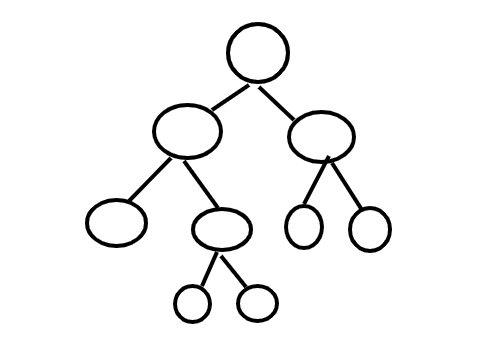
- Perfect binary tree:每個內部節點都有兩個子節點,且深度相同。
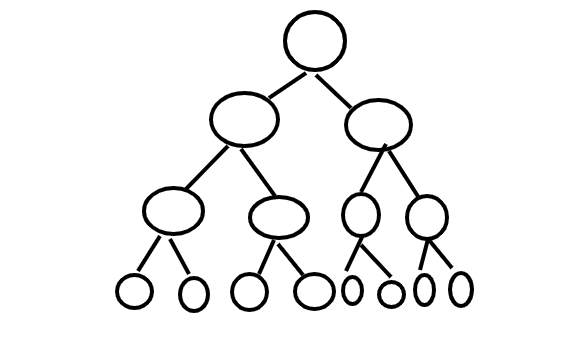
- Complete binary tree:所有層級上的節點都必須填滿,除了最後一層級。在最後一層級上,所有節點都必須向左對齊。
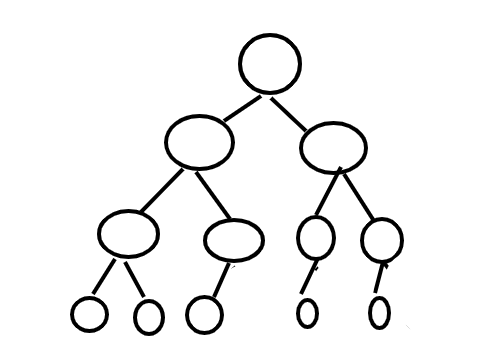
- Degenerate binary tree:樹長的像歪斜狀,每個節點都只有一個子節點。

- Binary Search Tree:每個節點都包含一個鍵value,且所有左子樹的鍵value都小於父節點的鍵value,所有右子樹的鍵value都大於父節點的value,左子樹和右子樹也必須是binary search tree。
DFS是什麼?
DFS的中文是深度優先搜索算法,從樹的root節點開始,儘可能深地訪問每個子樹,一層一層的執行,而不是先訪問所有的相鄰節點。DFS有兩種主要實現方式:iteratively和recursively。
- iteratively的DFS實現方式使用stack。從root節點開始,將其放入stack到中,然後不斷從stack最上面取出節點,擴展其相鄰節點,並將其放入stack中。當stack為空時,就代表所有的節點都已經被訪問。
- recursively的DFS實現方式通過遞迴實現。從root節點開始,遞歸地訪問每個子節點,直到訪問完整棵樹。在遞迴過程中,將每個節點標記為已訪問,以避免重複訪問。
iteratively的code大概會長這樣
node=root
stack=[]
while stack or node:
if node:
#vist
if not node.left is None and node.right is None
stack.append(node)
node = node.left
else:
node = stack.pop()
node = node.rightrecursively的code大概會長這樣
def recr(node):
if not node:
return
if node.left is None and node.right is None:
return
recr(node.left)
recr(node.right)recursively不同的是把東西存在memory stack(等同iteratively的stack)
memory stack效能會比stack稍微差一些,沒控制好的話會爆掉,所以最好在一進入function時候設一個中止條件。
中止條件
if not node
returndfs又分兩種寫法buttom-up和top-down ,buttom-up就是從最下一層往上推,推到最上面,慢慢組合想要的結果。top-down就是由上往下推,以下Leetcode題目會用buttom-up去做,因為看起來比較簡潔。
112. Path Sum

104. Maximum Depth of Binary Tree
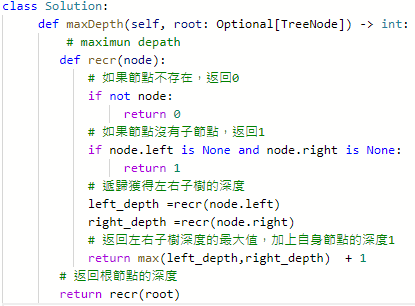
簡化的版本

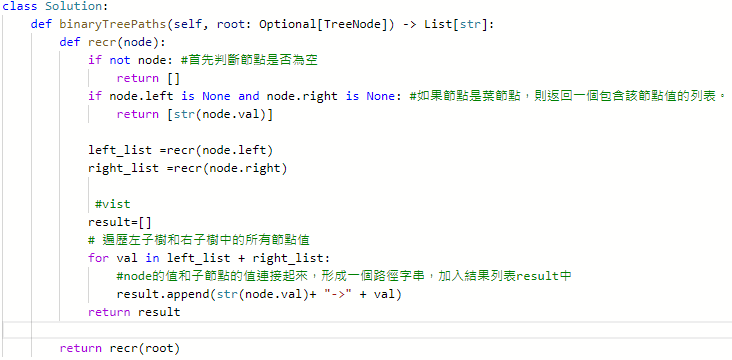
257. Binary Tree Paths
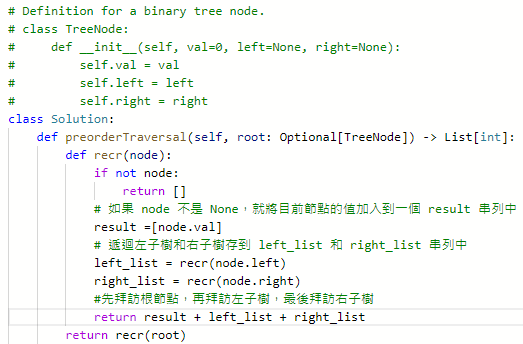
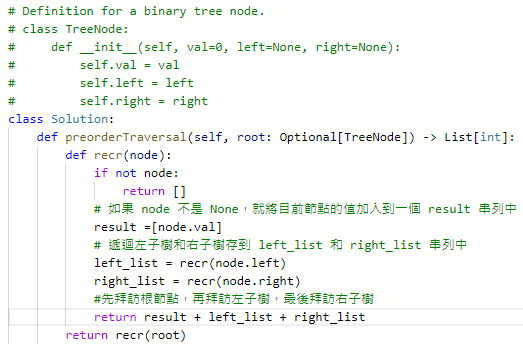
144. Binary Tree Preorder Traversal
100. Same Tree
700. Search in a Binary Search Tree