Divide-and-Conquer是將一個大問題分成一個較小的子問題。
Divide:將大問題分成幾個較小的子問題,小問題通常與大問題結構相似,但規模較小。
Conquer:遞歸解決較小的子問題。子問題足夠簡單的話,可以直接求解。
Combine:將較小的子問題的解合併起來,得到大問題的解。
Divide-and-Conquer 是一種寫bottom-up的方式,思考方向是一樣的。因為是把問題固定拆成K等分 ,所以時間複雜度就是O(nlogn) ,空間複雜度就是O(logn)。
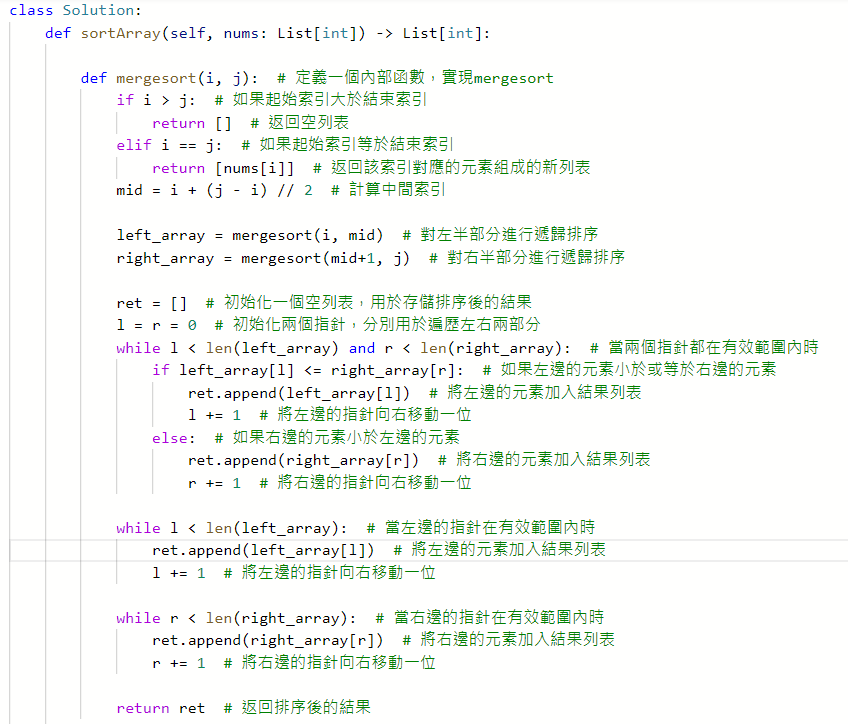
Merge Sort
將待排序的數組從中間分成兩個子數組。如果數組只有一個元素,那麼就不需要再分解了。
使用Merge Sort對兩個子數組進行遞迴排序。遞迴的結束條件是數組的大小為1,此時直接返回該數組。最後將兩個排序好的子數組合併成一個數組,特性是比較stable。
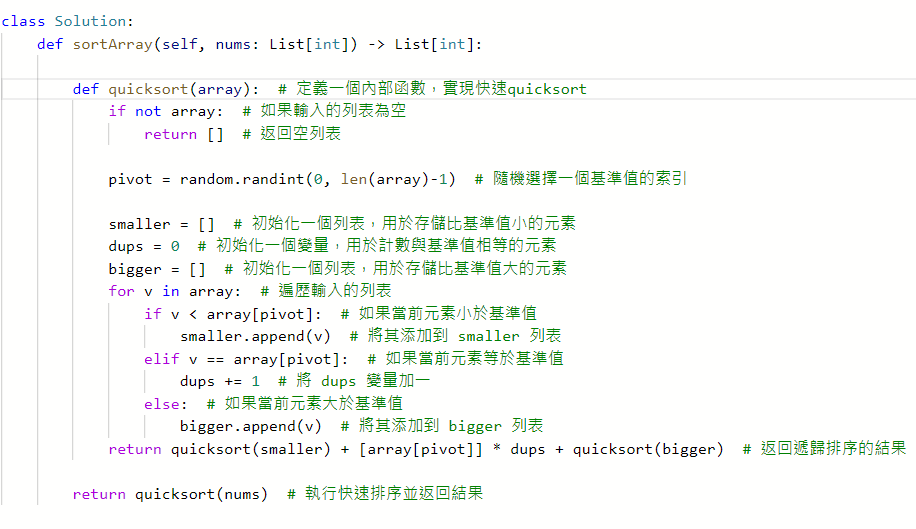
Quick Sort
從數組中選擇一個元素作為基準值。
重新排列數組,使得基準值的左側元素都比基準值小,基準值的右側元素都比基準值大。(比我大排右,比我小排左邊)對基準值左側和右側的兩個子數組進行遞迴排序。recr(右邊)+分水嶺+recr(左邊)
因為快速排序是原地排序演算法(不需要額外的存儲空間),所以合併的操作實際上並不需要。
時間複雜度:因為是隨機從數組中選擇一個元素作為基準值,所以不一定,若每次都挑到最小就衰,最壞就n2,平常情況下大部分是,跑幾百次幾千次會比較好,會比Merge Sort好一些,特性是比較not stable。
Quick Select
Quick Sort的一種變種,常用於解決「查找第K個元素」或「查找前K個元素」這類問題。
從數組中選擇一個元素作為基準值。
重新排列數組,使得基準值的左側元素都比基準值小,基準值的右側元素都比基準值大。
而不同於快速排序的是,快速選擇在分解後,會確定基準值在數組排序後的確定位置k。如果k等於我們要找的第K個元素,那麼直接返回該元素;如果k小於K,那麼在基準值的右側數組中查找第K-k個元素;反之,在基準值的左側數組中查找第K個元素。
Quick Select的時間複雜度在最壞情況下為O(n2),但在平均情況下為O(n)。
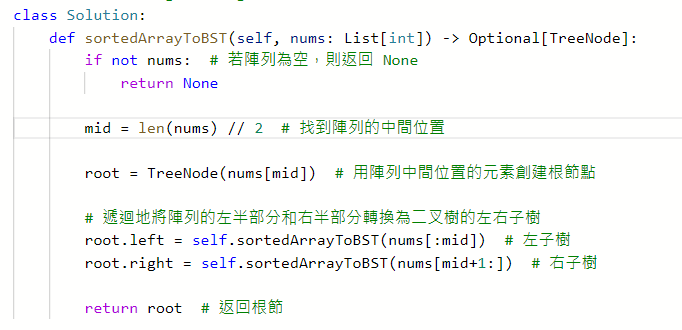
108. Convert Sorted Array to Binary Search Tree
Merge Sort
191. Number of 1 Bits
Merge Sort

1763. Longest Nice Substring
Merge Sort
