Line Sweep是以一定的方向(通常是從左至右或者由下至上),用一條虛擬的線(掃描線)掃過整個空間,並對掃描線與各種物體(如點、線、面)的交點或交界進行處理和計算。
這個方法可以解決許多幾何問題,例如計算平面上兩兩相交的線段數量,或者找出一堆矩形的聯合面積。掃描線演算法能將這些問題的時間複雜度降低到近線性。
在進行掃描的過程中,我們通常會維護一個稱為”活動結構”(Active Structure)的數據結構,如優先隊列或平衡樹,來保存和管理目前掃描線所遇到的物體,以便進行各種操作。
比如要計算一堆矩形的聯合面積。首先,會把每個矩形的左邊緣和右邊緣都作為一個事件點。左邊緣事件表示一個矩形的開始,右邊緣事件表示一個矩形的結束。每個事件點都有一個對應的變化量,表示在這個點上矩形的高度。
然後,把所有的事件點按照x軸的座標進行排序。接著,從左到右依序掃描每一個事件點。對於每個事件點,根據它的變化量來更新當前的活動結構(如一個保存著目前所有開始但還未結束的矩形的數據結構)。在兩個連續的事件點之間,就可以利用當前的活動結構來計算這個區間內的聯合面積。
這種方法的優點是只需要處理一次每個事件點,而且每次處理都是局部的,只需要考慮和當前事件點相關的矩形。所以,這種方法的時間複雜度通常比較低。
作法:
- 先把所有變化量都記下來
- 按照順序取變化量,得到答案
可以用兩種方法來解決 Array 以及 Hashmap + Sort
Array
就像是在每一個位置都放一個筆記本,每次有事情發生就在那個位置的筆記本上做記錄。好處是查找起來很快,但如果位置很多的話,就需要很多筆記本,能會很浪費空間。
作法:
1. 創建一個涵蓋所有範圍的Array ,把變化值都記錄下來
2. 再由小到大去拜訪 (時間 or 軸)
時間複雜度: O(n)
空間複雜度: O(n)
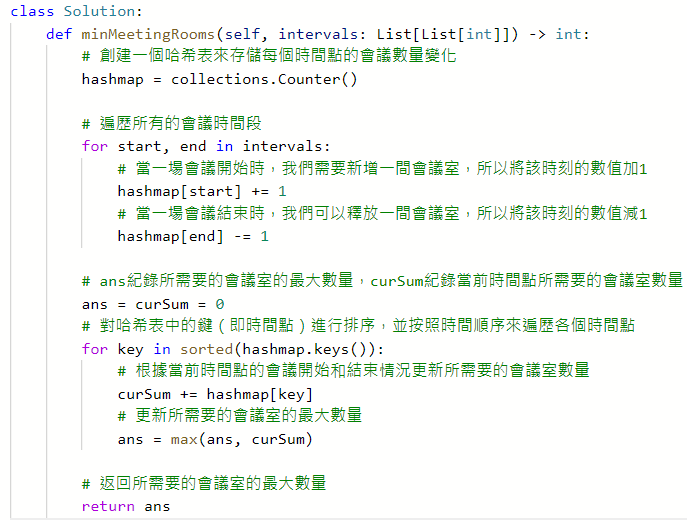
253. Meeting Rooms II

Hashmap + Sort
就像是在手上有一本筆記本,不管在哪裡發生事情,都在手上的這本筆記本做記錄,並且寫清楚是在哪裡發生的。這樣的好處是節省筆記本,不過需要的時候要先把筆記本的內容按照位置排序過(sort)才能找到想要的信息,但如果輸入的數據量翻倍則會比Array慢一點。
1. 創建一個hashmap,key是時間 or 軸,把變化值都記錄下來
2. 再sort hashmap的key,依照key去拜訪
時間複雜度: O(nlogn)
空間複雜度: O(n)
253. Meeting Rooms II
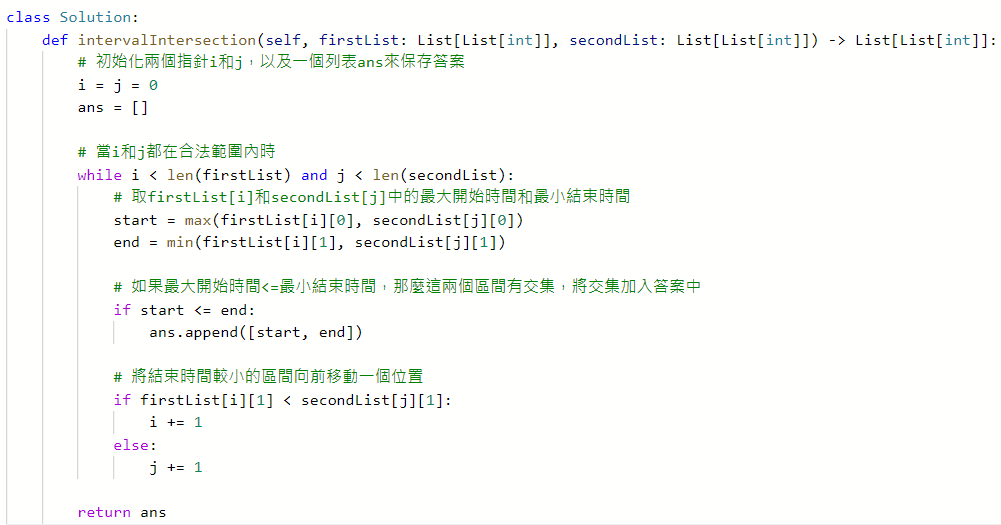
986. Interval List Intersections
1094. Car Pooling

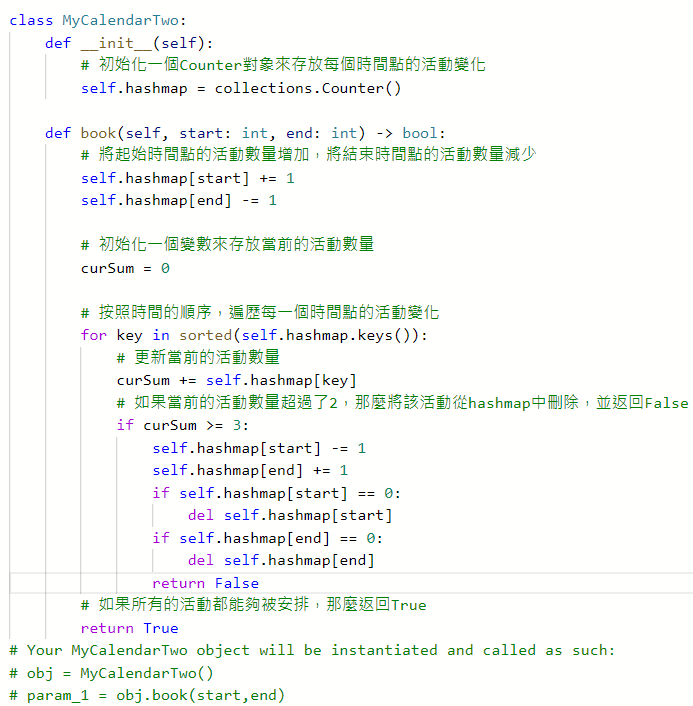
731. My Calendar II
370. Range Addition

1943. Describe the Painting
