Prefix Sum
把一串數字(例如:1, 2, 3, 4)從左到右每次都加上前面的數字,所形成的新數列就是Prefix Sum。例如在這個例子中,Prefix Sum就會是(1, 1+2, 1+2+3, 1+2+3+4),也就是(1, 3, 6, 10)。這樣做的好處是,如果要求某段數列(例如:2到4)的和,就可以直接拿Prefix Sum的第4項(10)扣除Prefix Sum的第1項(1),就能得到答案(9)
Prefix Sum是一種dynamic programming。 可以降低查詢範圍總和的時間複雜度。
Suffix Sum
則是從右邊開始計算的Prefix Sum。還是以同樣的數列(1, 2, 3, 4)為例,我們從右邊開始,每次加上前面(右邊)的數字,所形成的新數列就是Suffix Sum。在這個例子中,Suffix Sum就會是(1+2+3+4, 2+3+4, 3+4, 4),也就是(10, 9, 7, 4)。Suffix Sum的好處與Prefix Sum類似,只是適用的範圍不同。
Prefix Sum的題目
303. Range Sum Query – Immutable

1031. Maximum Sum of Two Non-Overlapping Subarrays

1991. Find the Middle Index in Array

1413. Minimum Value to Get Positive Step by Step Sum

Prefix Sum + hash map的題目
如果想找到子數組總和等於k的個數,可以使用presum+hash map
525. Contiguous Array
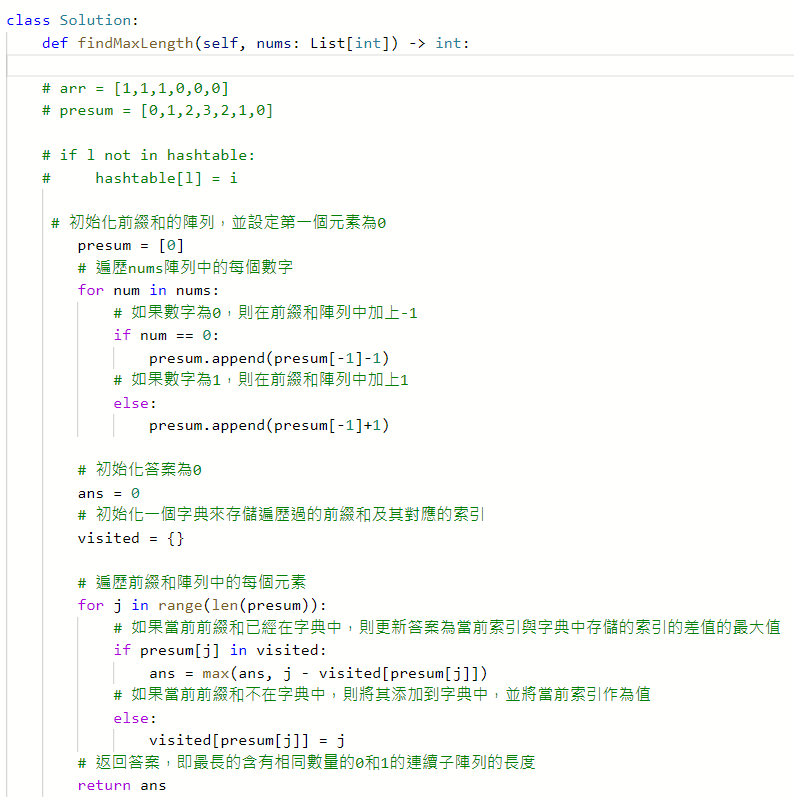
370. Range Addition

560. Subarray Sum Equals K
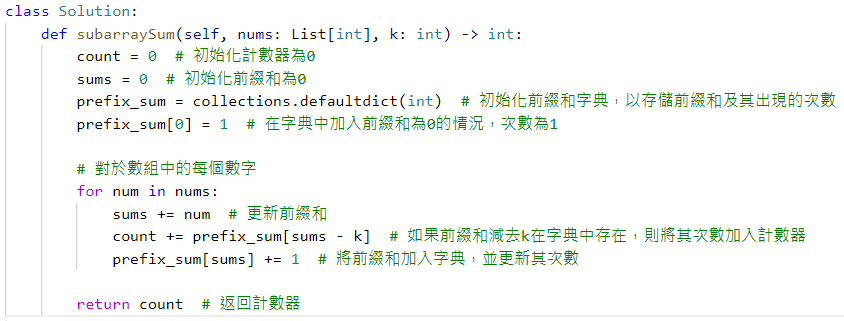
437. Path Sum III
