Preorder Inorder Postorder (Morris)

binary tree的遍歷方式可以分成Preorder、Inorder、Postorder這三種。

遍歷順序

Preorder：首先訪問root節點，然後遞歸地訪問左子樹和右子樹。

以下訪問的順序是[ 8 → 6 → 5 → 2 → 7 →15 →11 →9 →14 →18 → 22　]

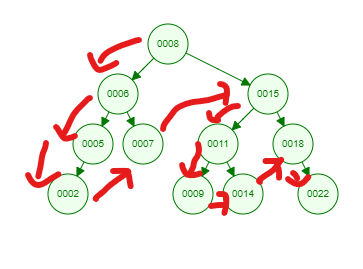
Inorder：首先遞歸地訪問左子樹，然後訪問root節點，最後遞歸地訪問右子樹(口訣：左中右)。

以下訪問的順序是[ 2 → 5 → 6 → 7 → 8 →9 →11 →14 →15 →18 → 22　]

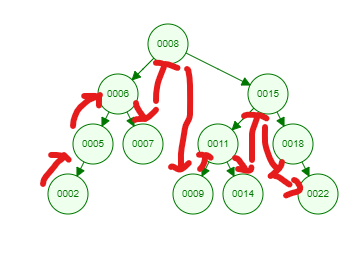
Postorder：首先遞歸地訪問左子樹和右子樹，然後訪問root節點(口訣：左右中)。

以下訪問的順序是[ 2 → 5 → 7 → 6 → 9 →14 →11 →22 →18 →15 → 8　]

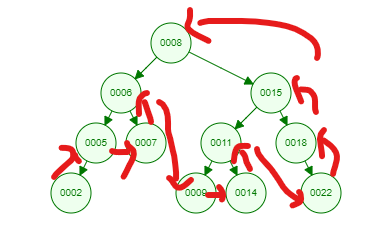
Iteratively 和 recursively的寫法

Preorder：首先訪問1.root節點，然後遞歸地訪問2.左子樹和3.右子樹

Iteratively

root  = node = Tree()
stack = []
while stack or node:
	if node:
		# visit
		print(root.val)     # 1.root
		stack.append(node) 
		node = node.left    # 2.left
	else:
		node = stack.pop()
		node = node.right   # 3.right

recursively

def recur(node):
	if not node:
		return
	# visit
	print(node.val)        # 1.root
	recur(node.left)       # 2.left
	recur(node.right)      # 3.right
recur(root)

Inorder：首先遞歸地訪問1.左子樹，然後訪問2.root節點，最後遞歸地訪問3.右子樹(口訣：左中右)。

Iteratively

root  = node = Tree()
stack = []
while stack or node:
	if node:
		stack.append(node)
		node = node.left     # 1.left
	else:
		node = stack.pop()
		# visit
		print(root.val)      # 2.root
		node = node.right    # 3.right

recursively

def recur(node):
	if not node:
		return
	recur(node.left)       # 1.left
	# visit
	print(node.val)        # 2.root
	recur(node.right)      # 3.right

Postorder：先遞歸地訪問1.左子樹和2.右子樹，然後訪問3.root節點(口訣：左右中)。

Iteratively

# iteratively
root  = node = Tree()
ans = []
stack = []
while stack or node:
	if node:
		# visit
		ans.append(node.val)  # 1→3.root
		stack.append(node)
		node = node.right     # 2→2.right
	else:
		node = stack.pop()
		node = node.left       # 3→1.left
ans.reversed()                 # 返回列表的逆序迭代器

recursively

def recur(node):
	if not node:
		return
	recur(node.left)       # 1.left
	recur(node.right)      # 2.right
	# visit
	print(node.val)        # 3.root

為什麼需要不同的遍歷方式呢？

每種遍歷方式都可以用來解決不同的問題。

Preorder可以用來建立一個二叉樹的複製

在Preorder中，root節點會先被遍歷，其次遍歷左子樹，最後遍歷右子樹。因此，如果已經知道了一棵二叉樹的Preorder結果，就可以通過結果構造出一棵與原本Binary Tree結構完全相同的Binary Tree。

Inorder可以用來得到一個有序的序列

在Inorder中首先遍歷左子樹，然後遍歷root節點，最後遍歷右子樹。由於Binary Search Tree( BST）的左子樹上所有節點的值都小於它的根節點的值；右子樹上所有節點的值都大於它的根節點的值且左右子樹也分別為二叉搜索樹。因此結果就是一個有序序列。若希望的結果的排序為有序序列可以使用Inorder。

Postorder：可以用來釋放一個二叉樹的所有節點。

在Postorder中首先遍歷左子樹，然後遍歷右子樹，最後遍歷root節點。由於在遍歷完左子樹和右子樹後再訪問root節點，因此可以釋放一個二叉樹的所有節點。

關於Morris算法

這邊稍微提一下，之後再作補充。

Morris遍歷是一種時間複雜度為O(n)，空間複雜度為O(1)的二元樹訪問算法。

Morris也是有Preorder、Inorder、Postorder這三種遍歷方法。

以下是Morris訪問方式的特徵：

由於3的右子節點為空，所以可以在3的右子節點建立一條point到root(4)的連結，而7的右子節點為空，所以可以在7的右子節點建立一條point到root(8)的連結。