Priority queue是一種自動排序的數據結構,它的結構是一種Tree,在這種結構中,數據項目具有與之相關的”優先順序”。項目可以根據其優先順序從queue中添加,但每次只能取出當前的最小值或最大值。優先順序最高的項目位於queue的前端。如果兩個項目具有相同的優先順序,則根據它們在queue中的位置來決定哪一個被首先移除。
Priority queue在各種情況下都非常有用,允許元素具有優先權,並始終允許最高(或最低)優先級的元素首先出隊。例如,在操作系統中,優先隊列可以用於處理器的任務排程,在這裡,高優先級的任務會被優先處理。或者在圖形學中,它們用於找到最短路徑,如Dijkstra的算法。
優先順序隊列可以通過各種方式實現,如linked list、array、heap或者Binary tree等。其中heap是實現優先隊列最常見也是最高效的數據結構。最小堆(Min-Heap)和最大堆(Max-Heap)分別用來實現最小優先隊列和最大優先隊列。
Heap Tree
Heap Tree,也稱heap,是一種滿足特定性質的完全二叉樹(Complete Binary Tree),並且將其存儲在array中。對於在array中的每個節點,每個點的左子樹的索引位置可以由 2node+1 得到,每個點的右子樹的索引位置可以由 2node+2 得到(在這裡 node 表示的是數組索引)。同樣地,每個節點的父節點的索引位置可以由 (node-1) // 2 得到。
- 每個點的左子樹 =>2node+1
- 每個點的右子樹=> 2node+2
- 每個點的父節點=> (node-1) // 2
Heap的兩種主要類型:最小堆(Min-Heap)和最大堆(Max-Heap)。其中Max-Heap的性質是每個父節點的值都大於或等於其子節點的值;而Min-Heap的性質是每個父節點的值都小於或等於其子節點的值。在這種結構中,最大(或最小)元素始終在堆的根部,這使得我們能在常數時間內找到最大(或最小)元素。
- 在Min-Heap中,每個父節點的值都小於或等於其子節點的值,因此,根節點(即 arr[0])總是最小的元素。如果我們將最小堆視為一種優先隊列,並將元素的”小”視為其”優先級”,那麼我們可以通過”pop“操作來獲得當前的最小值。但我們不能確定左右子樹哪個大。
- 在最Max-Heap中,每個父節點的值都大於或等於其子節點的值,因此,根節點(即 arr[0])總是最大的元素。如果我們將最大堆視為一種優先隊列,並將元素的”大”視為其”優先級”,那麼我們可以通過”pop“操作來獲得當前的最大值。但我們不能確定左右子樹哪個小。
在這種情況下,
Min-Heap的程式碼結構
class MinHeap:
def __init__(self, arr):
self.arr = arr
self.heapify()
def heapify(self):
# 整理array
def push(self, val):
# 加入新的值
def pop(self):
# 回傳並移除self.arr[0]
如何使用heap tree
def push(self, val):
首先先處理def push(self, val):函數的部分
- arr.append(0)
- 向上,只要比parent小就交換,換到不能換 arr[i], arr[j] = arr[j], arr[i]
時間複雜度是O(logn)
空間複雜度是O(1)
class MinHeap:
def __init__(self, arr):
self.arr = arr
self.heapify()
def heapify(self):
# 整理array
def push(self, val):
self.arr.append(val)
while parent > curNode:
swap(arr[p], arr[cur])
cur = p
def pop(self):
# 回傳並移除self.arr[0]def pop(self):
接下來處理def pop(self):函數的部分
- 把頭跟尾交換
- 移除尾:arr.pop()
- 往下,挑child小的交換
class MinHeap:
def __init__(self, arr):
self.arr = arr
self.heapify()
def heapify(self):
# 整理array
def push(self, val):
self.arr.append(val)
while parent < curNode:
swap(self.arr[p], self.arr[cur])
cur = p
def pop(self):
swap(self.arr[0], self.arr[-1])
self.arr.pop()
while curNode < child1 or child2:
swap(self.arr[cur], self.arr[ch1 or ch2])
cur = ch1 or ch2def heapify(self):
最後來看def heapify(self):
- 往下:O(n) 從中間~頭的每個點都往下整理 (pop的話只需從頭開始往下整理)
class MinHeap:
def __init__(self, arr):
self.arr = arr
self.heapify()
def heapify(self):
for i in range(len(self.arr)//2, -1, -1):
siftDown(i)
def push(self, val): # 往上整理
siftUp(i)
def pop(self): # 往下整理
swap(self.arr[0], self.arr[-1])
siftDown(0)Python套件heapq
heapq是Python內建的一個模塊,提供了對heap的支援
heapq模塊只有只有minHeap
import heapq
arr = [0,1]
heapq.heapify(arr) # 列表arr轉換為heap,按heap的屬性重新排列列表元素。
heapq.heappush(arr, 10) # 此函數將數值10添加到heap arr中
val = heapq.heappop(arr) # 此函數從heap arr中移除並返回最小的元素
要想實現Max-Heap(即父節點的值大於或等於其子節點的值),可以在push和pop元素時,對元素的值取負。因為對所有元素取負後,原來的最大值就變成了最小值,原來的最小值就變成了最大值,這樣就可以利用heapq模塊實現的Min-Heap來模擬Max-Heap的行為。
253. Meeting Rooms II
Min Heap

1167. Minimum Cost to Connect Sticks
Min Heap

973. K Closest Points to Origin
Max Heap

703. Kth Largest Element in a Stream
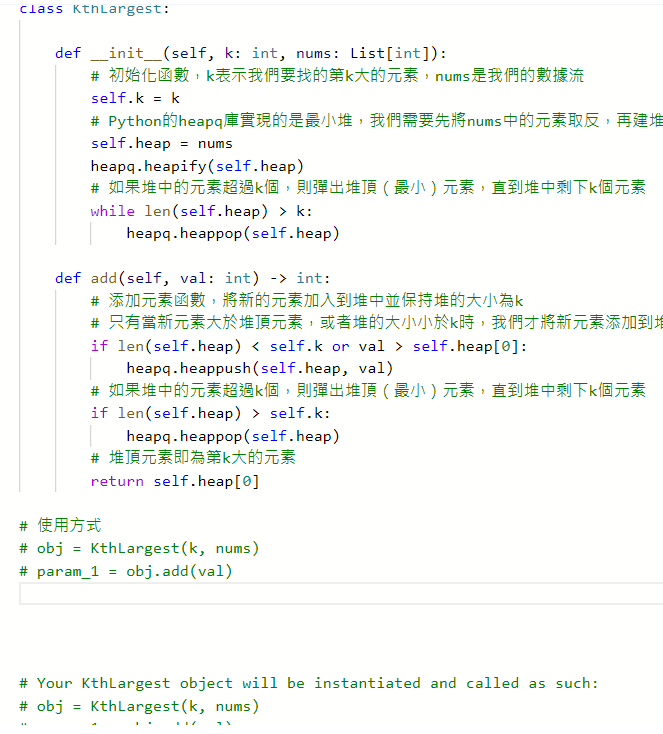
1046. Last Stone Weight

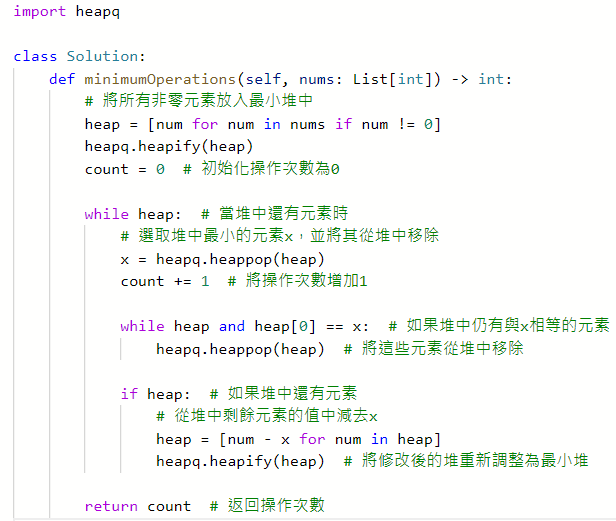
2357. Make Array Zero by Subtracting Equal Amounts