Pruning
剪枝是一種在搜索算法中優化搜索過程的方法,假設樹枝可能有10支 ,可以用一些判斷減少這些樹枝,例如回溯演算法、動態規劃、圖的搜索、遊戲理論中的min-max搜索等等。該方法是用if去減少搜索空間中我們確定或高度懷疑不會產生最佳結果的部分,以此減少搜索的空間範圍,加快演算法的運行速度。假設有很多選擇可以選,但有些選擇我們早就知道結果不會很好,所以就選擇不去走那條路,忽略不必要或者確定不好的選擇的方法,讓搜索過程更快,更高效。
Successor
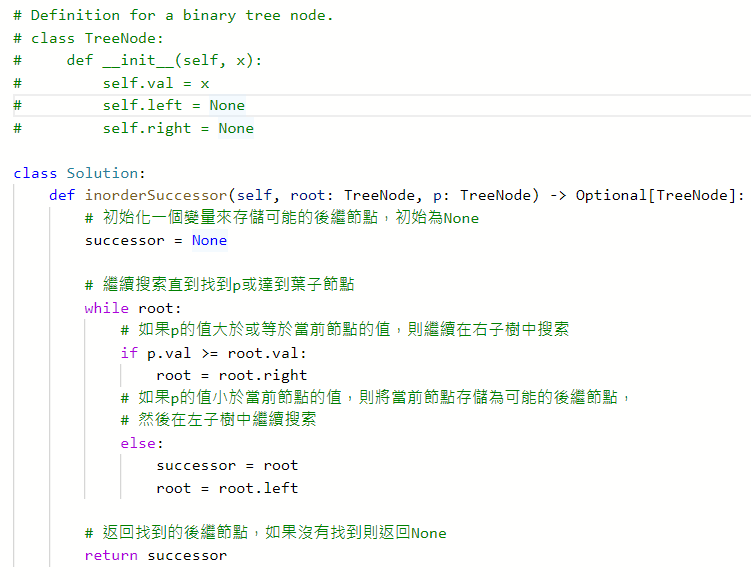
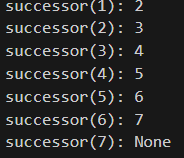
Successor常指某種排序或者搜索的上下文中,一個元素的”後一個”元素。例如,有一串數字如 1, 2, 3, 4,那麼在這個序列中,2 的Successor就是 3,因為 3 在 2 之後。在二元搜索樹中,一個節點的Successor可能是其右子樹中值最小的節點。
Predecessor
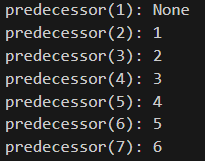
Predecessor是指在排序或者搜索的上下文中,一個元素的”前一個”元素。代表 “前一個” 或 “之前的”。以 1, 2, 3, 4 為例,在這個序列中,3 的 Predecessor就是 2,因為 2 在 3 之前同樣以二元搜索樹為例,一個節點的 Predecessor可能是其左子樹中值最大的節點,或者是在中序遍歷中,該節點之前的節點。
實際會用在什麼例子?
在 AI 的遊戲樹搜索中,常常會利用Pruning的策略來優化搜索過程,例如 alpha-beta 剪枝等。而在二元搜索樹、跳躍列表、哈希表等中,我們常常需要找到某個元素的Successor或Predecessor來進行插入、刪除或者搜索等操作。
Code的寫法
- Successor
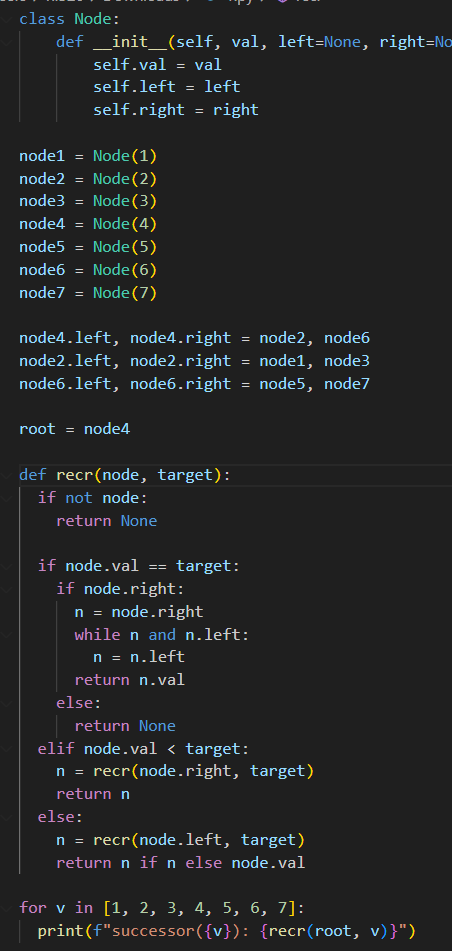
- Predecessor

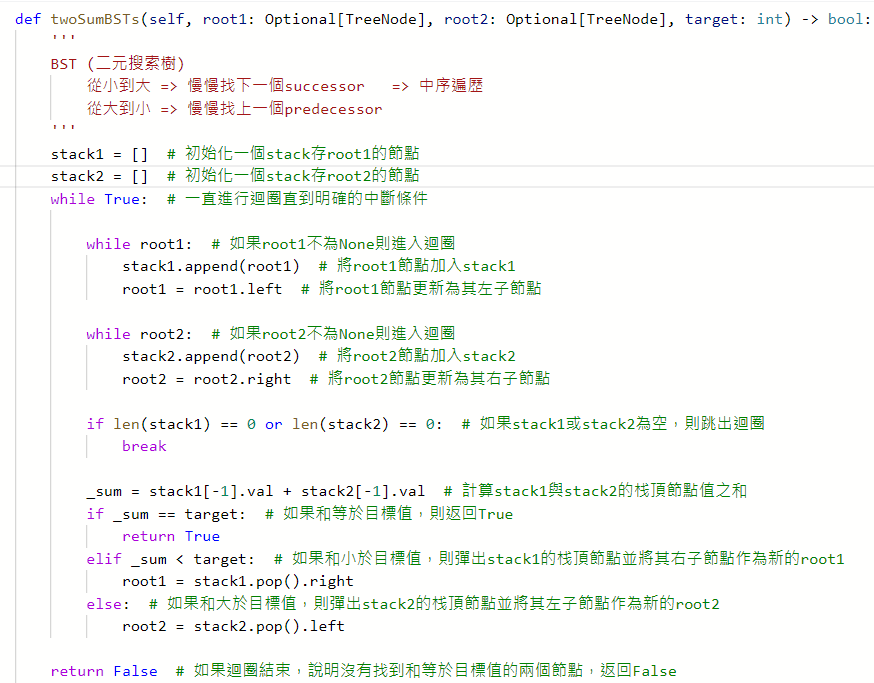
1214. Two Sum BSTs
39. Combination Sum(Pruning)

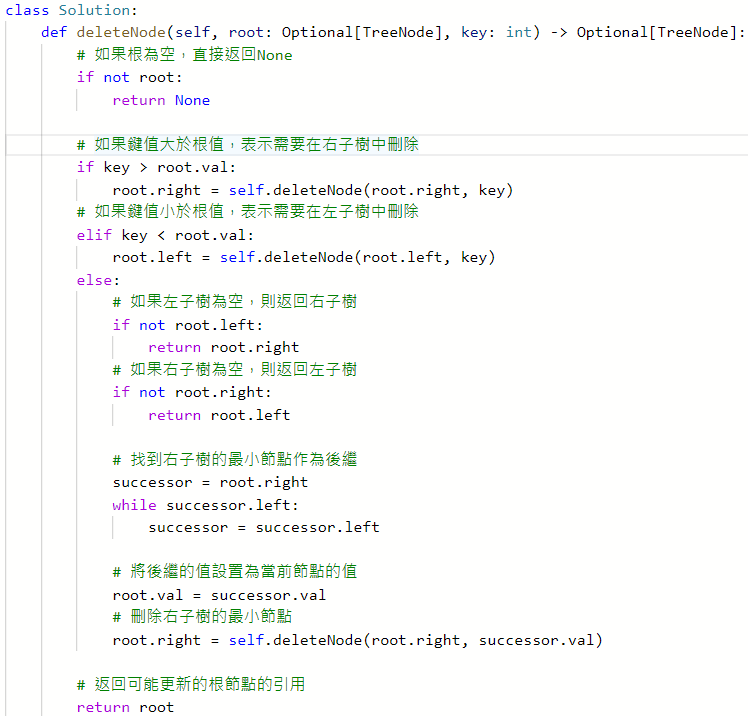
450. Delete Node in a BST(Successor & Predecessor)
285. Inorder Successor in BST(Successor & Predecessor)