Topological Sort是指將具有依賴關係的任務排序成一個序列,每個任務都在所有依賴任務完成後執用,來對有向無環圖(Directed Acyclic Graph, DAG)進行排序,使得對所有的有向邊(u, v),均有 u(在排序記錄中)比 v 先出現。若圖中存在環(Cycle),則該圖無法進行Topological Sort。
Topological Sort就是找出一種類似擋修之類的關係,先修完A才能修B,保證你都是先修完起點的課程才修終點的課程。這種算法會從一個沒有任何”擋修”關係的課程(也就是圖中入度為0的節點)開始,將這門課程加入排序的結果,然後移除與這門課程相關的”擋修”關係,重複這個過程,直到找出所有課程的選修順序。如果找不到這樣的選修順序(也就是存在環路,如A擋B,B又擋A),則表示課程之間的”擋修”關係有誤,Topological Sort可用於解決具有依賴關係的問題且不限制只有一種答案。
時間複雜度和空間複雜度都是 O(V+E)。
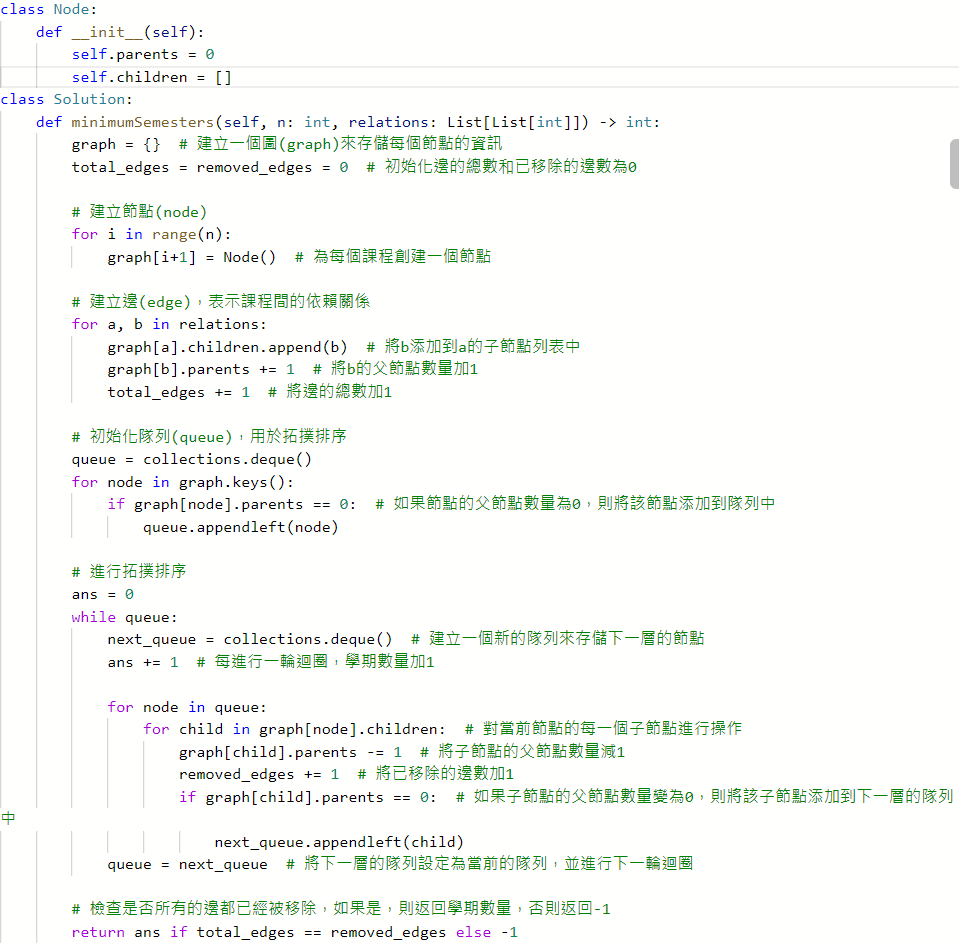
要如何做Topological Sort
定義好每個NODE要存的東西
- 每個點都要去記parent有幾個和children有誰
- 用一個queue去紀錄parent == 0的node
- pop queue,移除取出的這個node,把node的child的parent-1
210. Course Schedule II

269. Alien Dictionary

1136. Parallel Courses
310. Minimum Height Trees

207. Course Schedule

802. Find Eventual Safe States

851. Loud and Rich
